Limita

Z Multimediaexpo.cz

Tento článek pojednává o limitě funkce nebo zobrazení. O limitě a kolimitě v teorii kategorií je článek Limita (teorie kategorií)

Limita je matematická konstrukce, vyjadřující, že se hodnoty zadané posloupnosti nebo funkce blíží libovolně blízko k nějakému bodu. Právě tento bod je pak označován jako limita. Tato skutečnost se u funkcí zapisuje \(\lim_{z\rightarrow z_0} f(z)=a\) a u posloupností \(\lim_{n\to\infty} a_n=a\) případně \(a _n \to a\,\). Dle toho, zda se uvažuje o posloupnosti nebo o funkci, hovoříme o limitě posloupnosti nebo limitě funkce. Pojem limity lze definovat na libovolném metrickém prostoru.

Obsah

Limita posloupnosti

Hlavní článek: Limita posloupnosti

Posloupnost \(\left( a_n \right) _{n=1} ^\infty\) má limitu A, pokud se jejími hodnotami můžeme k A libovolně přiblížit. Tedy pro každé kladné číslo \(\varepsilon\) platí, že existuje nějaký člen posloupnosti, od kterého jsou už její hodnoty od A vzdáleny méně, než \(\varepsilon\). Zapsáno symbolicky:

\(\forall \varepsilon > 0: \exists n \in \mathbb{N} : \forall k \geq n : \left| a _k - A \right| < \varepsilon\)

Limita funkce

Hlavní článek: limita funkce

Říkáme, že funkce f(x) má v bodě a limitu A, jestliže k libovolnému \(\epsilon >0\) existuje takové \(\delta > 0\) , že pro všechna x z \(\delta\)-okolí bodu a, z něhož vyjmeme bod a (tzv. prstencová okolí bodu a) je \(\left| f(x)-A \right|< \epsilon, \).

Limita vzhledem k podmnožině

(Speciální případ: Pravostranná a levostranná limita)

Vlastní a nevlastní limita

Limitou posloupnosti může být nejen číslo (tj. vlastní limita), ale i symbol \(+\infty \,\!\) nebo \(-\infty \,\!\) (nevlastní limita). Limitu funkce lze zkoumat ve vlastním bodě (v reálném čísle), tak i v nevlastním bodě \(+\infty \,\!\) nebo \(-\infty \,\!\). V obou případech může být limita vlastní, nevlastní nebo limita nemusí existovat.

Zobecnění pro topologické prostory

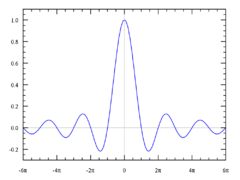
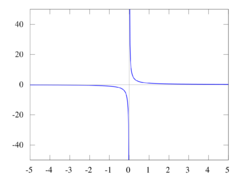
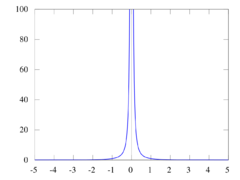
Limita zobrazení \(f: A\to B\) mezi topologickými prostory je v bodě a definována jako \(b\in B\) takové, že pro každé okolí O(b) bodu b existuje okolí O(a) bodu a takové, že \(x\in O(a)\) implikuje \(f(x)\in O(b)\). Dalším zobecněním limity posloupnosti, funkce i zobrazení jsou limity sítí[1]. Limita zobrazení nebo sítě může být v obecném topologickém prostoru víceznačná. Platí však, že v Hausdorffově prostoru, je tato limita jednoznačná, t.j. každá síť má nejvýše jednu limitu.

Příklady

Graf funkce \(\scriptstyle f(x) = \frac{\sin(x)}{x}\). Je vidět, že tato funkce má limitu 1 v bodě nula.

Graf funkce \(\scriptstyle f(x) = \frac{1}{x} \). Je vidět, že tato funkce nemá limitu v bodě nula a má vlastní limity 0 v \(\scriptstyle \pm \infty\).

Graf funkce \(\scriptstyle f(x) = \frac{1}{x^2}\). Je vidět, že tato funkce má nevlastní limitu \(\scriptstyle +\infty \,\!\) v bodě nula a má vlastní limity 0 v \(\scriptstyle \pm \infty\).

  • Funkce \({\sin x}\over x \,\!\) není v nule definovaná, ale má v ní limitu 1[pozn 1] (vlastní limita ve vlastním bodě) a v \(+\infty \,\!\) má limitu 0 (vlastní limita v nevlastním bodě).
  • Funkce \({\sin x} \,\!\) je v nule spojitá (limita je 0) a v \(+\infty \,\!\) limitu nemá. Obě tato tvrzení platí i o funkci \({x \cdot \sin x} \,\!\)
  • Funkce \({\sin {1\over x}} \,\!\) ani \({\sin {1\over x}}\over x \,\!\) v nule limitu nemají. Totéž platí i o funkcích \({1\over x}\,\!\) či \({1\over x^3}\,\!\), ovšem ty mají alespoň jednostranné limity: jejich pravostranná limita je \(+\infty \,\!\) a levostranná \(-\infty \,\!\). Naproti tomu funkce \({1\over x^2}\,\!\) a \({1\over x^4}\,\!\) mají v nule limitu \(+\infty \,\!\) (nevlastní limita ve vlastním bodě).
  • Funkce \(e^x\,\!\) má v \(-\infty \,\!\) limitu 0 (vlastní limita v nevlastním bodě) a v \(+\infty \,\!\) limitu \(+\infty \,\!\).

Poznámky

  1. ↑ To lze intuitivně zdůvodnit tak, že funkce sin x má v okolí nuly "velmi podobný" průběh, jako funkce f(x) = x; proto se jejich poměr blíží k jedné.

Související články

Reference

  1. ↑ Michael C. Gemignani, Elementary topology, Courier Dover Publications, 1990 (strana 122, def. 3)


Citováno z „http://www.multimediaexpo.cz/mmecz/index.php/Limita“