Multimediaexpo.cz je již 18 let na českém internetu !!
Kosinová věta
Z Multimediaexpo.cz
| Tento článek potřebuje úpravy. Můžete Multimediaexpo.cz pomoci tím, že ho vylepšíte. Jak by měly články vypadat, popisují stránky Vzhled a styl a Encyklopedický styl. |
|
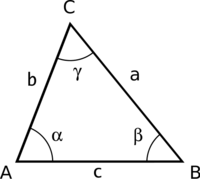
V trigonometrii je kosinová věta tvrzení o rovinných trojúhelnících, které umožňuje spočítat úhel v trojúhelníku na základě znalosti všech jeho tří stran.
Pro každý trojúhelník ABC s vnitřními úhly α, β, γ a stranami a, b, c platí:
- \(a^2 = b^2 + c^2 - 2 b c \cdot \cos \alpha\)
- \(b^2 = c^2 + a^2 - 2 c a \cdot \cos \beta\)
- \(c^2 = a^2 + b^2 - 2 a b \cdot \cos \gamma\)
Speciálním případem kosinové věty je Pythagorova věta: pokud je úhel γ pravý, pak \(\cos \gamma = 0\) a tudíž \(c^2 = a^2 + b^2\).
Větu lze mimo jiné použít v případě, že máme dány dvě strany trojúhelníku, úhel, který svírají, a chceme zjistit délku zbývající strany.
Důkaz
Důkaz vzorce pro zjištění strany a trojúhelníku ABC je vhodné rozdělit podle velikosti daného úhlu α (ostrý, pravý a tupý).
- Je-li α ostrý a bod P patou výšky vc, pak bod P náleží straně c (pokud ne, prohodíme označení bodů B a C). Vzdálenost paty P od bodu A označíme u. Pak podle Pythagorovy věty je
- \(a^2 = v_c^2 + (c-u)^2\).
- Protože dále platí, že \(u = b \cos \alpha\) a \(v_c = b \sin \alpha\), lze psát
- \(a^2 = (b \cdot \sin \alpha)^2 + (c - b \cdot \cos \alpha)^2\)
- \(a^2 = b^2 \cdot \sin^2 \alpha + c^2 - 2bc \cdot \cos \alpha + b^2 \cdot \cos^2 \alpha\)
- \(a^2 = b^2 (\sin^2 \alpha + \cos^2 \alpha) + c^2 - 2bc \cdot \cos \alpha\)
- \(a^2 = b^2 + c^2 - 2 b c \cdot \cos \alpha\)
- Je-li α pravý, pak podle pythagorovy věty je
- \( \ a^2 = b^2 + c^2\).
- Protože je α = π/2, je \(\cos \alpha = 0\), a pak
- \(a^2 = b^2 + c^2 = b^2 + c^2 - 2 b c \cdot \cos \alpha\)
- Je-li α tupý a bod P patou výšky vc, pak bod P leží mimo c. Vzdálenost paty P od bodu A označíme u. Pak podle Pythagorovy věty je
- \(a^2 = v_c^2 + (c+u)^2\)
- Protože dále platí, že \(u = b \cos (\pi - \alpha)\) a \(v_c = b \sin (\pi - \alpha)\) a dále \(\cos (\pi - \alpha) = -\cos \alpha\) a \(\sin (\pi - \alpha) = \sin \alpha\) lze psát
- \(a^2 = (b \cdot \sin \alpha)^2 + (- b \cdot \cos \alpha + c)^2\)
- Což je totéž, jako v případě, že je úhel α ostrý a tedy
- \(a^2 = b^2 + c^2 - 2 b c \cdot \cos \alpha\)
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |